[백준 1463번][C++] 1로 만들기

<문제 소개>

---

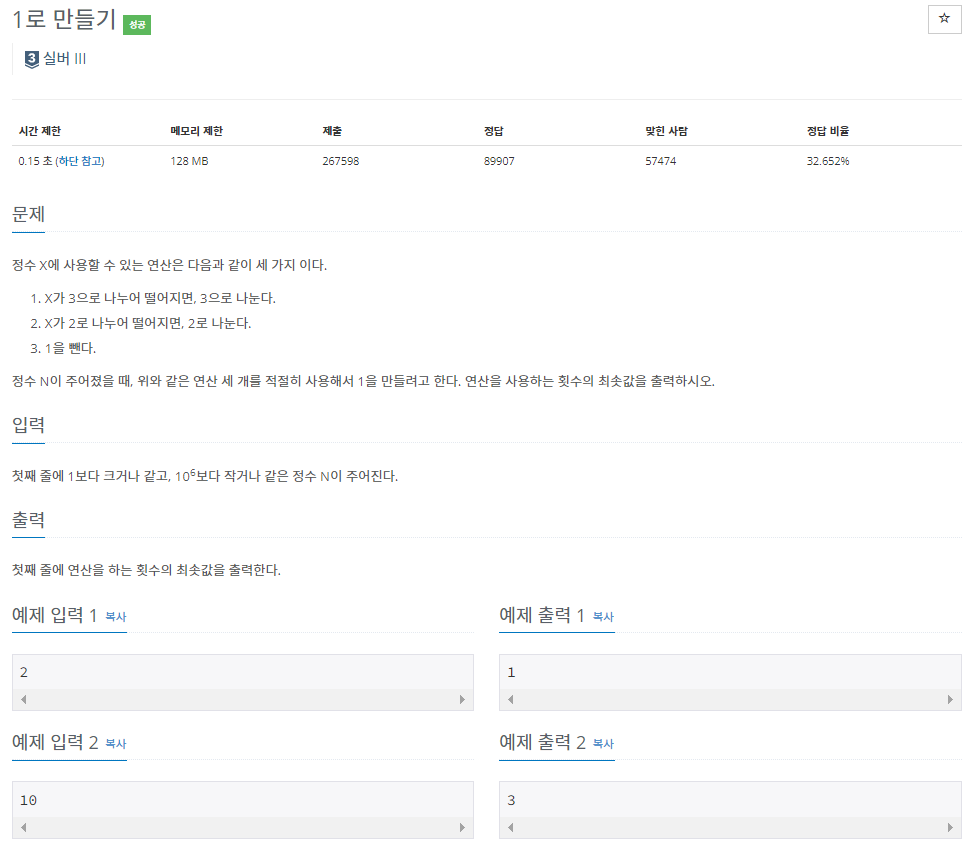
<소스 코드>

#include <iostream>
#include <string>
#include <vector>
#include <sstream>
#include <map>
#include <unordered_map>
#include <set>
#include <cmath>
#include <stack>
#include <queue>
#include <algorithm>
#include <cstdlib>
using namespace std;

int main()
{
	// 쓰레드 환경이 아닐때 버퍼를 분리하여 처리속도를 빠르게 해줌
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N;
	cin >> N;

	vector<int> dp(N + 1);

	// 2 -> 1 => 1
	// 3 -> 1 => 1
	// 4 -> 2 or 4 -> 3 => 1 + dp(2) or 1 + dp(3)
	// 5 -> 4 => 1 + dp(4)
	// 6 -> 3 or 6 -> 2 => 1 + dp(3) or 1 + dp(2)
	// 7 -> 6 => 1 + dp(6)
	// 8 -> 4 (or 8 -> 7) => 1 + dp(4) (< 1 + dp(7))
	// 9 -> 3 => 1 + dp(3)
	// 10 -> 9 or 10 -> 5 => 1 + dp(9) (< 1 + dp(5))

	// 규칙
	// 1. 2와 3으로 모두 나누어 떨어지지 않는 경우 -> ex) 5, 7		
	// -> 1(1을 빼주는 연산 횟수) + i-1에 저장된 최소 연산 횟수
	// 2. 2와 3으로 모두 나누어 떨어지는 경우 -> ex) 6				
	// -> 2로 나누어지는 연산 횟수(i/2)와 3으로 나누어지는 연산 횟수(i/3) 중 작은 횟수 + 1(6이 나누어지는 횟수)
	// 3. 2로만 나누어 떨어지는 경우 -> ex) 2, 4, 8, 10				
	// -> i/2 연산 횟수와 i-1 연산 횟수 중 작은 값
	// 4. 3으로만 나누어 떨어지는 경우 -> ex) 3, 9					
	//-> i/3 연산 횟수와 i-1 연산 횟수 중 작은 값
    
	dp[2] = 1;
	dp[3] = 1;

	for (int i = 4; i <= N; i++)
	{
		if (i % 2 != 0 && i % 3 != 0)
		{
			// 2와 3으로 모두 나누어 떨어지지 않는 경우
			dp[i] = 1 + dp[i - 1];
		}
		else if (i % 2 == 0 && i % 3 == 0)
		{
			// 2와 3으로 모두 나누어 떨어지는 경우
			dp[i] = 1 + min(dp[i / 2], dp[i / 3]);
		}
		else if (i % 2 == 0)
		{
			// 2로만 나누어 떨어지는 경우
			dp[i] = 1 + min(dp[i / 2], dp[i - 1]);
		}
		else if (i % 3 == 0)
		{
			// 3으로만 나누어 떨어지는 경우
			dp[i] = 1 + min(dp[i / 3], dp[i - 1]);
		}
	}
	
	cout << dp[N];

	return 0;
}

---

<풀이과정>

- 이전 과정을 계속 저장해나가면서 푸는 방법이다.(dp/bottom-up)

- 코드에 푸는 방법이 적혀있어 풀이과정은 생략한다.

---

<코멘트>

dp문제를 풀어보았는데 처음이라 그런지 아직 익숙하지도 않고 어렵기도 해서 못풀었다ㅠㅠ

그래서 다른 분들의 풀이를 보고 풀었다!

---

<제출결과>