반응형
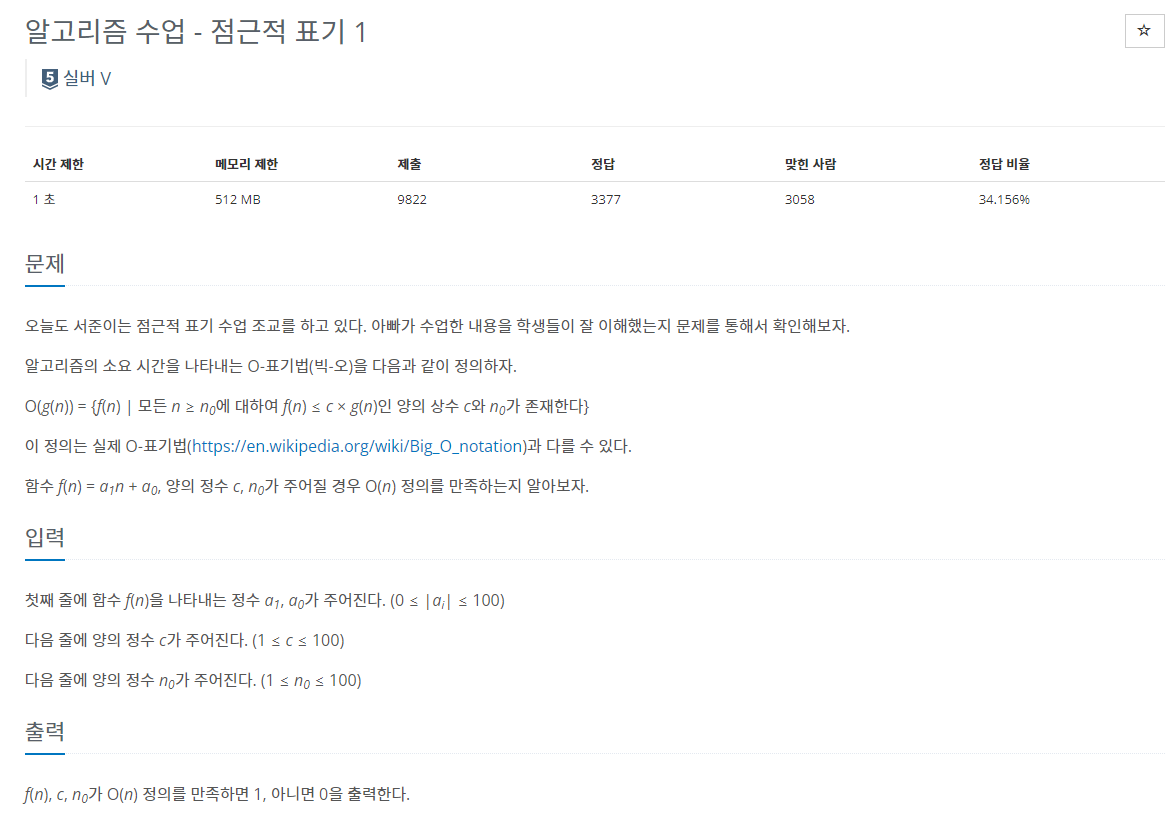
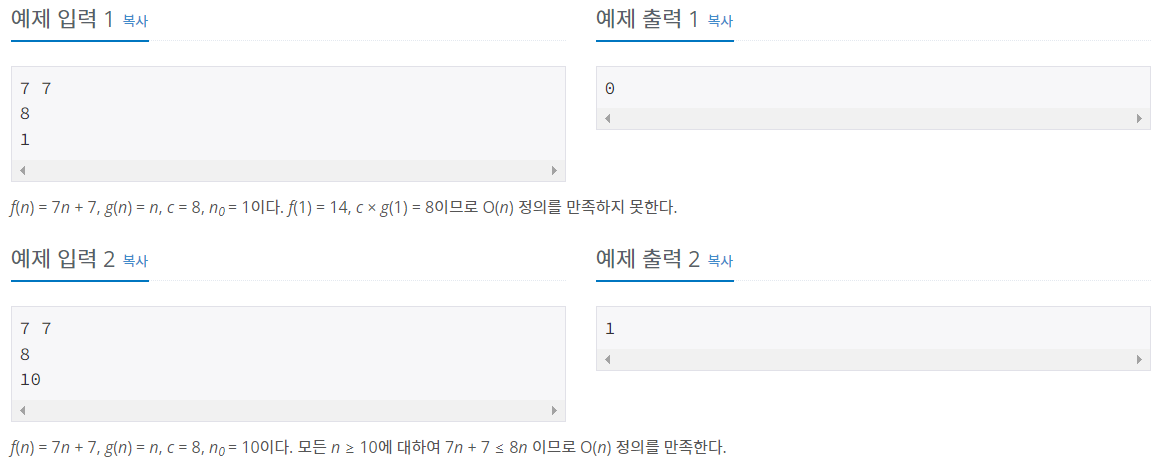
<문제 소개>
<소스 코드>
#include <iostream>
#include <string>
#include <vector>
#include <sstream>
#include <map>
#include <cmath>
#include <stack>
#include <queue>
#include <algorithm>
#include <cstdlib>
using namespace std;
int main()
{
int result = 0;
int a1, a0, c, n0;;
cin >> a1 >> a0;
if (a1 > 100 || a1 < -100 || a0 > 100 || a0 < -100) return 0;
cin >> c;
if (c > 100 || c < 1) return 0;
cin >> n0;
if (n0 > 100 || n0 < 1) return 0;
// 1. f(x)의 기울기가 작거나 같은 경우 c >= a1 -> 교점 이후의 점들에서 성립
// -> f(k) == g(k)일때, k <= n0이면 1출력
// 2. f(x)의 기울기가 큰 경우 c < a1 -> 교점 이전의 점들에서 성립
// -> n >= n0가 성립하는 경우가 없음 -> 0출력
if (c >= a1)
{
// ax +b = cx -> x = b/(c-a)
float k = a0 / (float)(c - a1);
if (k <= n0)
{
result = 1;
}
}
cout << result;
return 0;
}<풀이과정>
1. 입력값들을 받아옴
2. 경우의 수를 파악
3. f(x)의 기울기와 g(x)의 기울기를 비교(g(x) = x라고 생각하면 됨)
4-1. f(x)의 기울기가 작거나 같은 경우
- c >= a1
- 교점 이후의 점들은 모두 f(x)<= g(x)이므로 성립가능
- 그러므로 f(k) = g(k)일때, k>= n0이면 성립 -> 1출력
4-2.f(x)의 기울기가 더 큰 경우
- c < a1
- 교점 이전의 점들이 모두 f(x)<= g(x)이므로 성립 불가능(n0 이상인 수들이 만족해야하기 때문)
5. 위의 조건에 맞게 경우의 수를 나누어 판단하여 result값을 넣어준 뒤 출력
<코멘트>
문제를 해석하고 경우를 나누는 작업이 조금 헷갈리고 어려웠지만 한 번에 맞춰버렸다! 오예



