[백준 2750번][C++] 수 정렬하기 - 1. 버블 정렬

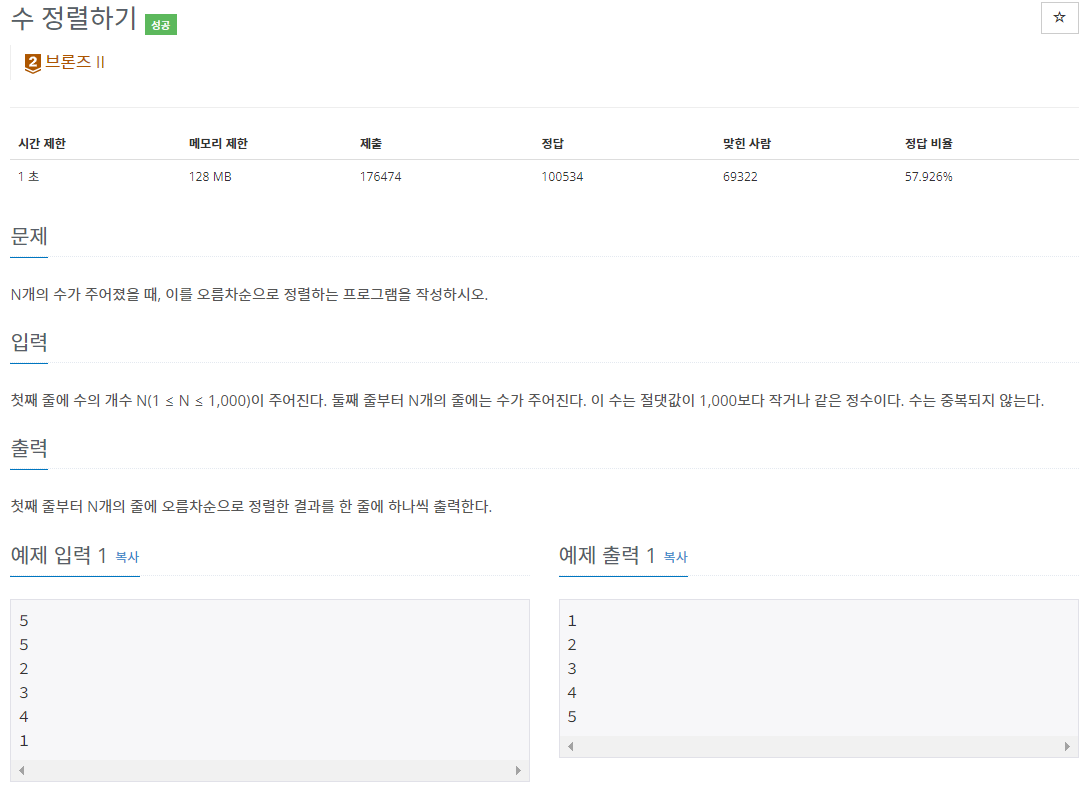
<문제 소개>

---

<소스 코드>

#include <iostream>
#include <string>
#include <vector>
#include <sstream>
#include <map>
#include <cmath>
#include <stack>
#include <queue>
#include <algorithm>
#include <cstdlib>
using namespace std;

int main()
{	
	int N; 
	cin >> N;

	vector<int> v;

	// 원소 입력
	while (N > 0)
	{
		int x;
		cin >> x;

		v.push_back(x);
		N--;
	}

	// 1. 버블 정렬
	for (int i = v.size() - 1; i > 0; i--)
	{
		for (int j = 0; j < i; j++)
		{
			if (v[j] > v[j + 1])
			{
				int temp = v[j];
				v[j] = v[j + 1];
				v[j + 1] = temp;
			}
		}
	}

	// 원소 출력
	for (int i = 0; i < v.size(); i++)
	{
		cout << v[i] << endl;
	}

	return 0;
}

---

<풀이과정>

1. 마지막부터 원소가 정렬되므로 점점 비교해나가는 사이즈를 줄여나가야함

2. 그러므로 i를 벡터 v의 원소들의 갯수와 같게 시작해서 1보다 작아질때까지 감소시키면서 진행

3. j는 0부터 i-1까지 v의 원소들을 돌면서 인접한 원소들끼리의 크기비교를 진행한다.

4. v[j]가 v[j+1]보다 크다면 둘의 값을 바꿔주는 것으로 한 반복이 끝나면 가장 큰 수가 맨 마지막에 위치하도록 한다.

5. 모든 반복이 끝나면 v의 원소들은 오름차순으로 정렬이 완료되어있다.

---

<코멘트>

이제부터 이 정렬문제를 통해 모든 정렬을 구현해볼것이다!

첫번째로 버블정렬로 푼 방법이다!

 

- 버블 정렬 -

장점 : 구현이 쉬움, 코드가 직관적

단점 : 시간복잡도가 최악이든 최선이든 O(n^2)을 갖기에 효율적이지 않음

특징 

1. 시간복잡도 O(n^2)

2. 공간복잡도 O(1)

3. in-place정렬 

4. stable정렬

 

<cf>

1. stable vs not-stable

- stable 정렬은 중복된 키 값이 있을 때 이를 순서대로 정렬하는 알고리즘을 뜻함

- 즉 , 정렬했을 때 중복된 키 값이 원래 순서대로 정렬되어있으면 stable 아니면 not-stable이다.

2. in-place vs not in-place

- in- place 정렬은 원소들의 개수에 비해 충분히 무시할 만한 저장 공간만을 더 사용하는 정렬 알고리즘을 뜻함.

- not in-place 정렬은 원소들의 개수에 비례하여 저장 공간을 더 사용하는 정렬 알고리즘을 뜻함.

---

<제출 결과>

<버블 정렬>