[프로그래머스][C++] 하노이의 탑

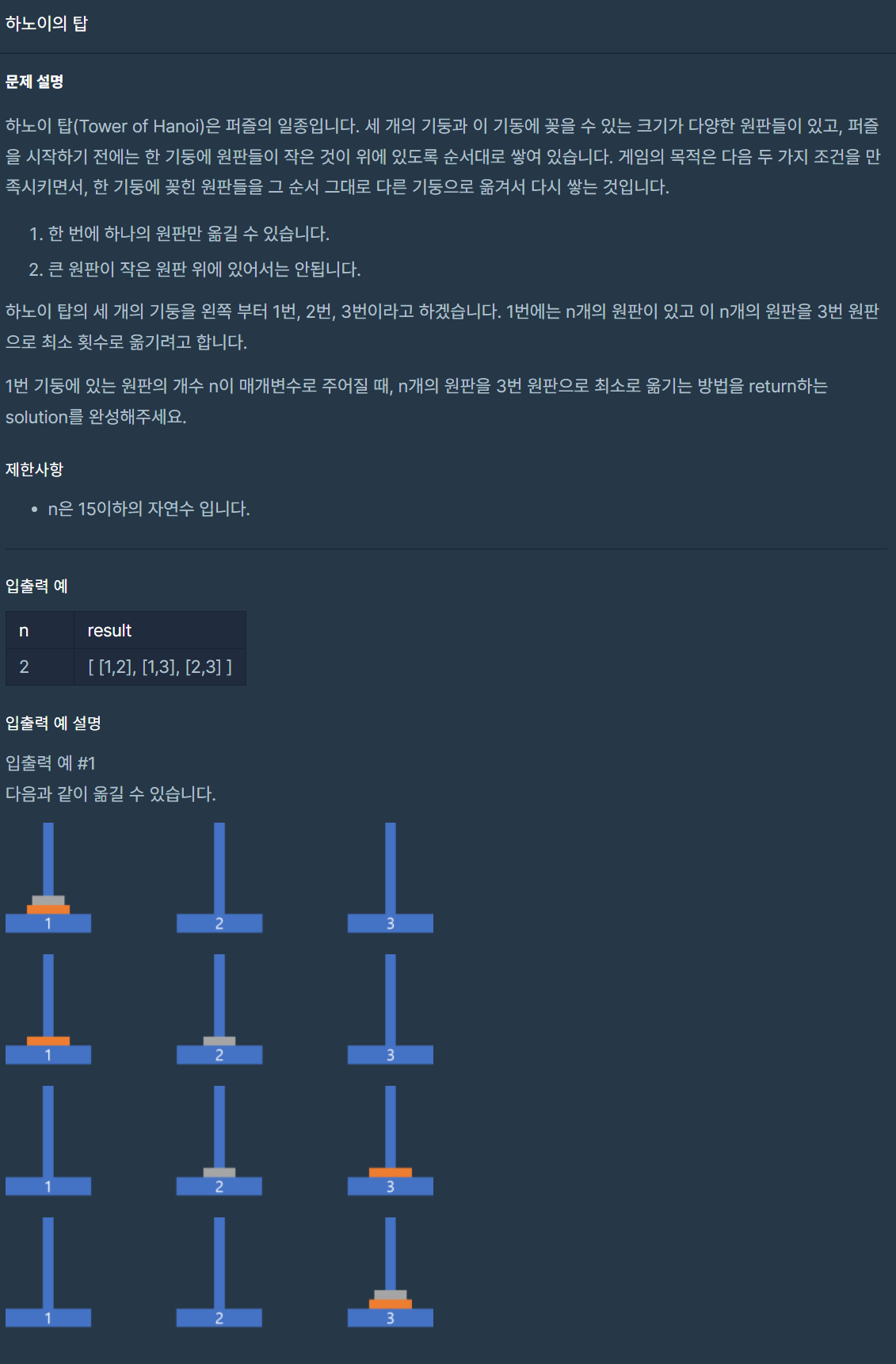
<문제 소개>

---

<소스 코드>

#include <string>
#include <vector>

using namespace std;

vector<vector<int>> hanoi(int curNum, int n, vector<vector<int>> pred) 
{
    if(curNum == n) return pred;    
    curNum++;
    
    vector<vector<int>> curVec = pred;
    
    // 1. 이전 원판들을 2번으로 옮김(2와 3을 바꿈)
    for(int i = 0; i < pred.size(); i++)
    {
        if(pred[i][0] == 2)
        {
            pred[i][0] = 3;
        }
        else if(pred[i][0] == 3)
        {
            pred[i][0] = 2;
        }
        
        if(pred[i][1] == 2)
        {
            pred[i][1] = 3;
        }
        else if(pred[i][1] == 3)
        {
            pred[i][1] = 2;
        }
    }
    
    // 2. k번 원판을 1번에서 3번으로 옮김
    pred.push_back({1,3});
    
    // 3. 이전 원판들을 3번으로 옮김(1과 2를 바꾼 pred를 추가)    
    for(int i = 0; i < curVec.size(); i++)
    {
        if(curVec[i][0] == 1)
        {
            curVec[i][0] = 2;
        }
        else if(curVec[i][0] == 2)
        {
            curVec[i][0] = 1;
        }
        
        if(curVec[i][1] == 1)
        {
            curVec[i][1] = 2;
        }
        else if(curVec[i][1] == 2)
        {
            curVec[i][1] = 1;
        }
    }
    
    pred.insert(pred.end(), curVec.begin(), curVec.end());
    
    return hanoi(curNum, n, pred);
}


vector<vector<int>> solution(int n) 
{
    vector<vector<int>> answer;
    
    // n = 1
    answer.push_back({1,3});
    
    // n = 2
    // 1. 1번 원판을 2번으로 옮김 -> n=1의 과정에서 2와 3을 바꿈
    // 2. 2번 원판을 1번에서 3번으로 옮김 {1,3}
    // 3. 2번에 있는 1번 원판을 3번으로 옮김(2번에서 3번으로 옮김) -> n=1의 과정에서 1과 2를 바꿈
    
    // n = k
    // 1. k-1번째까지의 원판들을 2번으로 옮김 -> n=k-1의 과정에서 2,3을 바꿈
    // 2. k번 원판을 1번에서 3번으로 옮김 {k,3}
    // 3. 2번에 있는 k-1번째까지의 원판들을 3번으로 옮김 -> n=k-1의 과정에서 1,2를 바꿈 
    
    // 하노이의 탑 계산
    answer = hanoi(1, n, answer);    
    
    return answer;
}

---

<풀이과정>

1. n=1일 때의 옮기는 과정인 {1,3}을 answer 벡터에 추가해줌

2. hanoi함수를 이용해 원판의 갯수가 n개일 때의 과정을 구해 answer에 넣어준다.

 

<hanoi>

1. n번째 탑까지의 방법을 curNum이 n이 될때까지 재귀적으로 구함

2. 이전 벡터 pred를 받아와 curVec에 저장

3. 첫번째 과정으로 k-1번째까지의 원판들을 2번으로 옮기는 과정을 구해야한다.

4. k-1번째까지의 원판들을 1번에서 3번으로 옮기는 과정이 이전 과정이었으므로 1번에서 2번으로 옮기는 과정은 pred 순서쌍의 2와 3을 바꿔서 구할 수 있다.

5. 이 방법으로 첫번째 과정인 k-1번째까지 원판들을 1번에서 2번으로 옮길 수 있었고, 다음으로 이제 1번에 남은 k번째 원판 하나를 3번으로 옮겨주는 작업을 해준다.

6. 즉  {1,3}을 pred에 추가해준다.

7. 마지막으로 2번에 놔둔 k-1 번째까지의 원판들을 3번으로 옮기는 과정을 진행하는데 pred를 복사한 벡터 curVec을 이용해 2번에서 3번으로 옮기는 작업이므로 기존 순서쌍의 1과 2를 바꾸어 해당 과정을 구할 수 있다.

8. 이렇게 구한 curVec을 insert를 이용해 pred의 뒤에 이어준다.

9. 재귀적으로 다음 하노이 함수를 호출하고 curNum이 n이 될때까지 이 과정을 반복한다.

---

<코멘트>

조금 어려웠지만 원리를 생각해내니 풀 수 있었다.

---

<제출결과>