[백준 2485번][C++] 가로수

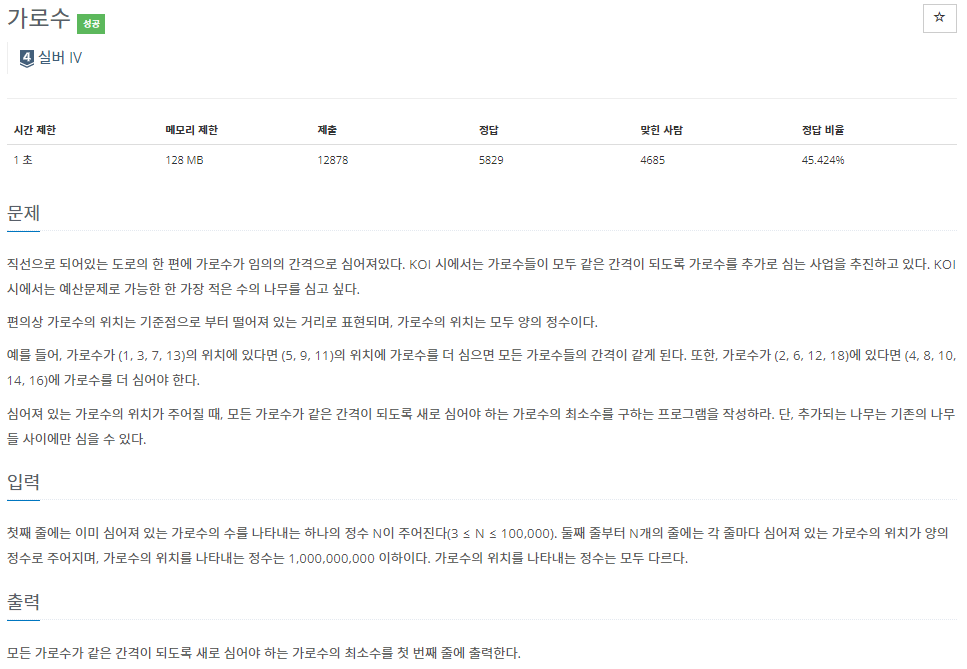
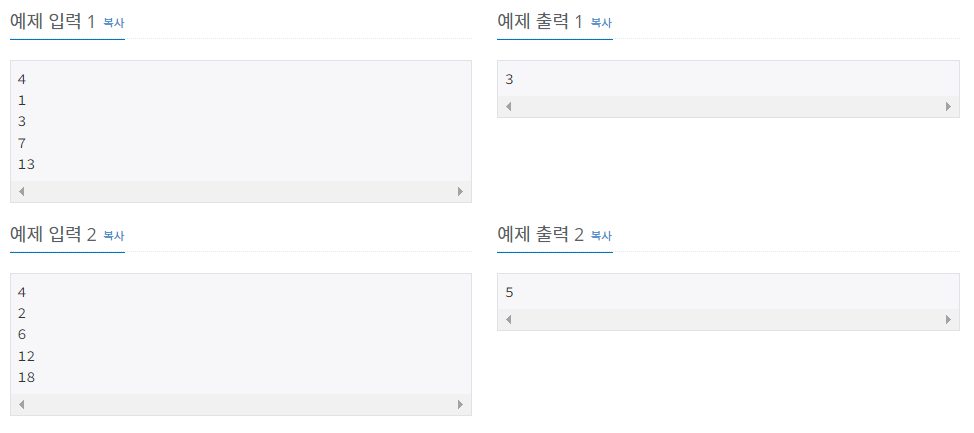
<문제 소개>

---

<소스 코드>

#include <iostream>
#include <string>
#include <vector>
#include <sstream>
#include <map>
#include <unordered_map>
#include <set>
#include <cmath>
#include <stack>
#include <queue>
#include <algorithm>
#include <cstdlib>
using namespace std;

int gcd(int big, int small)
{
	int r = big % small;

	if (r == 0) return small;
	else return gcd(small, r);
}

int main()
{
	// 쓰레드 환경이 아닐때 버퍼를 분리하여 처리속도를 빠르게 해줌
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N;
	cin >> N;

	vector<int> v(N);

	for (int i = 0; i < N; i++) 
		cin >> v[i];

	int GCD = v[1] - v[0];

	for (int i = 1; i < v.size() - 1; i++)
	{
		int nextDiff = v[i + 1] - v[i];

		int big = GCD > nextDiff ? GCD : nextDiff;
		int small = GCD == big ? nextDiff : GCD;

		GCD = gcd(big, small);
	}

	int count = 0;
	int curNum = v[0];

	for (int i = 1; i < v.size();)
	{
		if (curNum + GCD == v[i])
		{
			curNum = v[i];
			i++;
		}
		else
		{
			curNum += GCD;
			count++;
		}
	}

	cout << count;

	return 0;
}

 

---

<풀이과정>

1. N을 입력받고, N 크기의 벡터 v를 선언, N번 반복하며 입력을 벡터 v에 넣어줌

2. 최대공약수의 초기값을 v의 첫번째 원소와 두번째 원소의 차이로 설정

3. 각 수들의 차이값들의 최대공약수를 구할 것이고, 첫 수들의 차이값이 GCD로 설정되어 있으므로 두번째 수와 세번째 수의 차이값을 nextDiff라고 설정, GCD와 nextDiff 중 큰 값과 작은 값을 찾고, 유클리드 호제법을 이용해 두 수의 최대공약수를 구해준다.

4. 해당 최대공약수의 값을 GCD에 대입해주고, 다음 차이값과 GCD의 최대공약수를 구한다.

5. 이 과정을 마지막 직전 수와 마지막 수의 차이값까지 반복하여 각 차이값들의 최대공약수를 구할 수 있다.

6. 해당 최대공약수 GCD만큼 띄워가며 가로수를 세우면 되므로, 현재 세운 가로수의 갯수인 count를 0으로 초기화, 현재 가로수가 놓인 위치 curNum을 벡터 v의 첫번째 원소 v[0]으로 선언한 뒤, curNum부터 가로수를 세우기 시작한다.

7. curNum에 GCD를 더한 값이 벡터의 다음 원소 v[i]인 경우 curNum을 v[i]로 변경, i가 다음 원소를 가리키도록 i++을 해줌

8. 만약 curNum에 GCD를 더한 값이 v[i]가 아닌 경우 가로수를 세워야 하는 위치이므로 다음 위치인 curNum을 GCD를 더해 바꿔주고, 가로수의 갯수 count를 증가시켜준다.

9. 벡터 v의 원소의 갯수만큼 이 과정을 반복한 뒤 세운 가로수의 갯수 count를 출력해준다.

---

<코멘트>

음.. 최대공약수를 사용해서 풀어보았다!

사실 시간초과 나거나 틀릴줄 알았는데 맞춰서 기분이 좋았다!ㅋㅎㅋ

각 수들의 차이들의 최대공약수를 구하고 최대공약수만큼 가로수를 세웠다.

---

<제출결과>