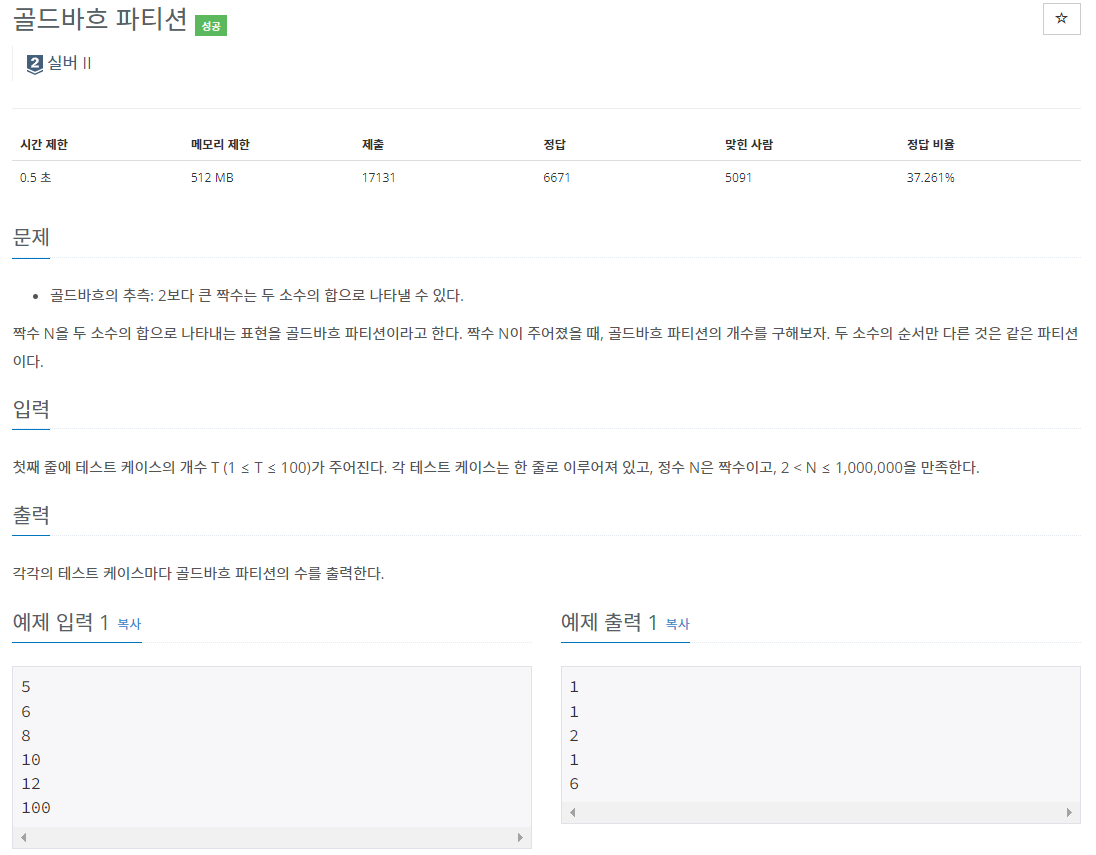
<문제 소개>
<소스 코드>
#include <iostream>
#include <string>
#include <vector>
#include <sstream>
#include <map>
#include <unordered_map>
#include <set>
#include <cmath>
#include <stack>
#include <queue>
#include <algorithm>
using namespace std;
void FindPrimeNumber(int maxVal, vector<bool>& primeNumbersCheck)
{
// 에라토스테네스의 체 공식
// -> 각 소수들의 배수를 지워나가며 찾는 방식
for (int i = 2; i <= maxVal; i++)
{
// 초기값을 true 설정
primeNumbersCheck.push_back(true);
}
for (int i = 2; i <= sqrt(maxVal); i++)
{
if (!primeNumbersCheck[i]) continue; // 이미 소수가 아닌 경우
for (int j = i * i; j <= maxVal; j += i)
{
// 소수가 아님
primeNumbersCheck[j] = false;
}
}
}
int GoldBachPartitionCount(int inputNum, vector<bool> primeNumbersCheck)
{
vector<int> primeNumbers;
int count = 0;
// inputNum보다 작은 소수들만 찾음
for (int i = 0; i < inputNum; i++)
{
// 소수만 담음
if (primeNumbersCheck[i]) primeNumbers.push_back(i);
}
for (int i = 0; i < primeNumbers.size(); i++)
{
// 주어진 수 - 소수 = 소수 -> 소수의 합으로 표현가능
// 따라서 [주어진수 - 소수]가 소수인지 확인
int checkNum = inputNum - primeNumbers[i];
if (primeNumbersCheck[checkNum])
{
// 소수들의 합은 결국 한 쌍이므로 두번씩 반복되게 되어있음
// 그러나 같은 수끼리 더하는 경우에는 반복체크가 안됨
// 같은 수끼리 더하는 경우에는 횟수체크를 한번더하고 마지막에 반으로 나눠줌
if (checkNum == primeNumbers[i]) count++;
count++;
}
}
return count / 2;
}
int main()
{
// 쓰레드 환경이 아닐때 버퍼를 분리하여 처리속도를 빠르게 해줌
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int T;
cin >> T;
vector<bool> primeNumbersCheck(2); // 0과 1은 false로 초기화
vector<int> input;
int maxVal = 0;
for (int i = 0; i < T; i++)
{
int N;
cin >> N;
maxVal = max(maxVal, N);
input.push_back( N);
}
// 최댓값까지의 소수들을 구함
FindPrimeNumber(maxVal, primeNumbersCheck);
// 골드바흐 파티션의 개수를 구함
for (int i = 0; i < input.size(); i++)
{
cout << GoldBachPartitionCount(input[i], primeNumbersCheck) << "\n";
}
return 0;
}<풀이과정>
1. T를 입력받고, 입력값들을 저장할 input 벡터를 선언하고, 각 인덱스의 해당하는 수들이 소수인지를 확인하는 primeNumberCheck를 선언하고, 0과 1은 소수가 아니므로 초기화할때 false로 초기화되는 점을 이용해 크기 2로 초기화하여 0번 인덱스와 1번 인덱스의 값을 넣어준다.
2. T만큼 반복하며 입력값들을 input에 저장하면서 가장 큰 값 maxVal를 찾아준다.
3. 반복하면서 구한 maxVal까지의 소수들을 FindPrimeNumber() 함수를 이용해 찾아준다.
4. input의 원소들을 돌면서 GoldBachPartitionCount() 함수를 이용해 각 원소의 골드바흐 파티션의 갯수를 구하고 바로 출력해준다.
- FindPrimeNumber
1. 인자로 int와 vector<bool>&을 받는다.
2. 최댓값 maxVal과 primeNumberCheck를 받아 maxVal까지의 수들 중 소수를 찾아주는 함수이다.
3. 먼저, primeNumbersCheck에 2번 인덱스부터 maxVal번 인덱스까지 true값으로 초기화시켜준다.
4. 에라토스테네스의 체 공식을 사용해 소수를 구한다.
5. 2부터 시작하여 maxVal의 제곱근까지 반복하며 각 수의 배수들은 소수가 아닌 점을 이용한다.
6. j = i * i 로 시작하는 이유 : i 이전의 값들에 대한 배수들은 구했기 때문
(ex. i = 10 -> 10 x 2는 2의 배수에서 구함)
7. maxVal의 제곱근까지만 반복하는 이유 : i * i 부터 배수인지 확인하는데 i * i 가 maxVal보다 커지면 배수 체크를 할 필요가 없음. 그러므로 i * i = maxVal이되는 i = sqrt(maxVal) 까지만 구함
(ex. maxVal = 100 -> i = 11이면 11x11 = 121이되므로 확인 할 필요 없음)
8. 위와 같은 방법으로 2부터 maxVal까지 반복하며 이미 소수가 아닌 경우는 넘어가고, 각 소수들의 배수들은 false로 바꾸는 과정을 반복하여 maxVal까지의 수들이 소수인지 확인할 수 있는 primeNumberCheck를 완성한다.
- GoldBachPartitionCount()
1. 인자로 int와 vector<bool>을 받는다.
2. 입력값 inputNum과 앞서구한 소수인지 확인하는 primeNumberCheck를 받아온다.
3. inputNum보다 작은 소수들만 담을 벡터 primeNumbers를 선언하고, 골드바흐 파티션의 갯수 count를 0으로 초기화 시켜서 선언한다.
4. inputNum보다 작은 수들을 반복하며 primeNumberCheck를 이용해 해당 수가 소수인 경우에만 primeNumbers에 담아준다.
5. 담은 소수들의 집합인 primNumbers의 원소들을 돌면서 입력된 수 inputNum과 현재 원소 primeNumbers[i]의 값의 차 checkNum이라고 선언하고 checkNum이 소수인지 확인할 것이다.
6. primeNumberCheck를 이용해 checkNum이 소수인지 확인하고 만약 소수인 경우에는 count를 1씩 증가시켜주는데 골드바흐 파티션에서 두 소수의 순서만 다르면 같은 파티션이기 때문에 이 경우에는 두 소수의 순서가 다른 것을 모두 세어 결국 총 2번 세는 꼴이 된다.
7. 이 점을 이용해 모든 반복이 끝난뒤 count를 반으로 나눈 값을 반환해주면 된다.
8. 하지만 5 + 5 = 10 과 같이 같은 수가 두 번 더해지는 경우는 한 번만 카운트되기 때문에 inputNum - primeNumer[i] = checkNum에서 checkNum과 primeNumbers[i]가 같은 경우에는 아예 카운트를 한 번 더 해준다.
9. 위와 같이 반복하면서 예외사항을 처리해준 뒤 반복이 끝나면 앞서 말한대로 골드바흐 파티션의 갯수인 count/2를 반환해준다.
<코멘트>
시간초과 때문에 엄청 애먹은 문제
소수 구하는 시간이 오래걸리는 거 같아서 에라토스테네스의 체 공식 사용해서 풀었는데도 계속 시간초과가 나왔다.
골드바흐 파티션에서 이중 for문으로 소수의 합들을 모두 구하는 데에서 시간이 낭비되는 것이었다.
입력된 수와 소수의 차이가 소수인지를 판단하는 생각을 해내는 것이 키 포인트 였다.
<제출결과>




