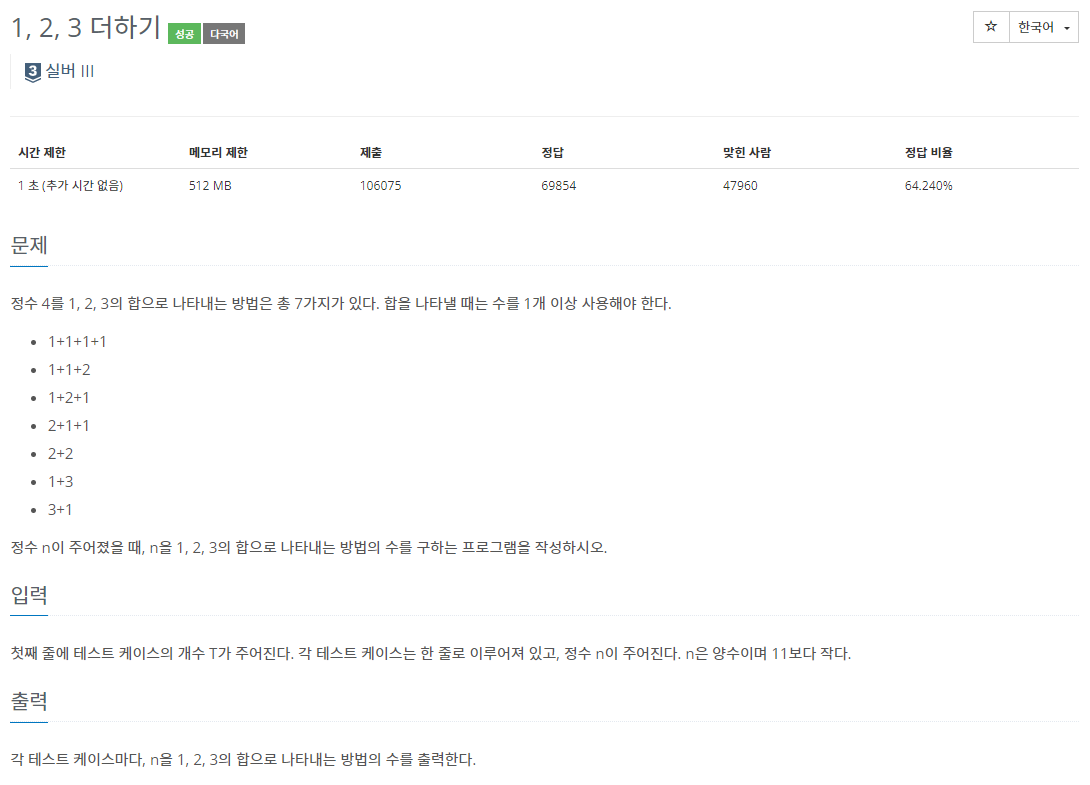
<문제 소개>

<소스 코드>
#include <iostream>
#include <string>
#include <vector>
#include <sstream>
#include <map>
#include <unordered_map>
#include <set>
#include <cmath>
#include <list>
#include <stack>
#include <queue>
#include <algorithm>
using namespace std;
int Combine(int n, int k)
{
// 조합을 계산
int x = 1; // 분자
int y = 1; // 분모
for (int i = 1; i <= k; i++)
{
x *= n - i + 1;
y *= i;
}
return x / y;
}
int main()
{
// 쓰레드 환경이 아닐때 버퍼를 분리하여 처리속도를 빠르게 해줌
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int T;
cin >> T;
vector<int> output(T);
for (int p = 0; p < T; p++)
{
int n;
cin >> n;
int count = 0;
// 1. 1로만 표현 -> 1가지
count++;
// 2. 2로만 표현 -> n/2 가지 방법
for (int i = 1; i <= n / 2; i++)
{
// i : 2의 갯수
int k = n - 2 * i; // 1의 갯수
// 2와 1로만 표현 -> 2의 갯수 i개, 1의 갯수 k개 -> nCi 개(조합)
int minVal = min(i, k);
count += Combine(i + k, minVal); // 조합의 갯수만큼 더해줌
}
// 3. 3으로만 표현 -> n/3 가지 방법
for (int i = 1; i <= n / 3; i++)
{
// i : 3의 갯수
int k = n - 3 * i; // 1의 갯수
int minVal = min(i, k);
count += Combine(i + k, minVal);
}
// 4. 2,3으로 같이 표현
// 4-1. 3의 갯수 k -> n - 3*k / 2 가지 방법
for (int i = 1; i <= n / 3; i++)
{
// i : 3의 갯수
int res = n - 3 * i; // 남은 수
if (res < 2) break; // 남은 수가 2보다 작은 경우
for (int j = 1; j <= res / 2; j++)
{
// j : 2의 갯수
int k = res - 2 * j; // 1의 갯수
// 1,2,3으로 표현됨
// 1,2를 같은 수로 생각한 뒤, 3과 1,2에 대해 조합의 갯수를 구하고 이후에 1,2의 조합의 갯수를 구함
count += Combine(i + j + k, min(i, j + k)) * Combine(j + k, min(j, k));
}
}
output[p] = count;
}
for (int i = 0; i < output.size(); i++)
{
cout << output[i] << "\n";
}
return 0;
}<소스코드 2>
#include <iostream>
#include <string>
#include <vector>
#include <sstream>
#include <map>
#include <unordered_map>
#include <set>
#include <cmath>
#include <list>
#include <stack>
#include <queue>
#include <algorithm>
using namespace std;
int main()
{
// 쓰레드 환경이 아닐때 버퍼를 분리하여 처리속도를 빠르게 해줌
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int T;
cin >> T;
vector<int> dp(12);
vector<int> output(T);
dp[1] = 1;
dp[2] = 2;
dp[3] = 4;
for (int i = 4; i <= 11; i++)
{
dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];
}
for (int p = 0; p < T; p++)
{
int n;
cin >> n;
output[p] = dp[n];
}
for (int i = 0; i < output.size(); i++)
{
cout << output[i] << "\n";
}
return 0;
}<풀이과정> - 경우의 수를 나누어 조합으로 푸는 방법
1. 1,2,3으로 표현하는 방법의 경우의 수는 크게 4가지로 나눌 수 있다.
1-1. 1로만 표현되는 방식 ex. 4 = 1+1+1+1
1-2. 2와 1로만 표현되는 방식 ex. 4 = 2+1+1
1-3. 3과 1로만 표현되는 방식 ex. 4 = 3+1
1-4. 1,2,3 모두를 이용해 표현되는 방식 ex. 7 = 3+2+1+1
2. 위의 4가지 방법으로 경우의 수를 나누어 구할 것이다.
3. 먼저 T를 입력받고, 각 결과값을 담을 output 벡터도 T의 크기로 선언한다.
4. T만큼 반복하며 n을 입력 받고, 각 입력마다 표현되는 방법의 수를 체크할 count를 0으로 초기화하여 선언해준다.
5. 첫번째 경우의 수
5-1. 1로만 표현되는 방식은 항상 1가지 이므로 count를 1 증가시켜준다.
6. 두번째 경우의 수
6-1. 2와 1로만 표현되는 방식은 2와 1의 갯수를 구하고 갯수들의 조합의 가짓수만큼 count에 더해주면 된다.
6-2. n/2 까지 2의 갯수를 표현할 수 있고, 2의 갯수는 0보다 커야 하므로, 1부터 n/2까지 반복문을 진행한다.
6-2. 위의 반복문의 반복자 i는 2의 갯수를 나타내므로, n에서 2*i를 빼주면 1의 갯수 k를 구할 수 있다.
6-3. 2와 1의 총 갯수 i+k과 i와 k중 더 작은 수를 이용하여 조합 계산을 진행하고 해당 수를 count에 더해준다.
6-4. 모든 i에 대해서 반복을 진행하며 count에 경우의 수를 더해준다.
7. 세번째 경우의 수
7-1. 3과 1로만 표현되는 방식은 2와 1로 표현되는 방식과 같은 방식으로 구할 수 있다.
8. 네번째 경우의 수
8-1. 1,2,3 모두를 이용해 표현되는 방식은 먼저 3의 갯수를 1부터 n/3까지 반복하고, n에서 3의 갯수만큼 빼고 남은 수를 res로 저장한다.
8-2. 만약 res가 2보다 작다면 남은 수는 1밖에 없는 것이므로 세번째 경우와 중복되기 때문에 계산하지 않고 넘어간다.
8-3. res가 2보다 크다면 res는 2와 1로 표현될 수 있기에 1부터 res/2까지 2의 갯수 j를 반복하며 경우의 수를 계산한다.
8-4. 1의 갯수 k는 res에서 2*j를 빼주어 구할 수 있다.
8-5. 이제 3의 갯수 i, 2의 갯수 j, 1의 갯수 k까지 모두 나온 상태이므로, i,j,k를 이용한 조합의 경우의 수를 계산하여 count에 더해주면 된다.
8-6. 먼저 크게 3과 나머지 수들이라고 생각하여 조합을 계산하고 나머지 수인 2와 1의 조합의 수를 계산해 둘을 곱을 구하여 count에 더해주면 된다.
8-7. 총 갯수 i+j+k에서 i와 j+k중 작은 수의 조합의 갯수를 구하고, 3을 뺀 j+k개에서 j와 k중 작은 수의 조합의 갯수를 구하여 곱해서 구할 수 있다.
8-8. 모든 i와 j의 대해서 반복을 진행하며 count에 경우의 수를 더해준다.
9. 한 숫자에 대해서 위의 과정이 끝나면 output 벡터에 count를 추가해준다.
10. 모든 숫자에 대해 count를 구한뒤 output에 저장된 count들을 하나씩 출력해준다.
- Combine()
1. 인자로 int n 과 int k를 받는다.
2. 조합은 n부터 n-k까지 하나씩 감소하며 곱해진 수를 1부터 k까지 하나씩 곱해진 수로 나눠서 구할 수 있다.
3. 그렇기에 먼저, 분자 x와 분모 y를 선언하고 1로 초기화 시켜준다.
4. 1부터 k까지 반복하며 분자 x에는 n-i+1을 곱해주고, 분모 y에는 i를 곱해주는 과정을 진행한다.
5. 마지막에 x/y를 리턴해 준다.
<풀이과정 2> - 점화식을 이용해 푸는 방식
1. 이 문제를 잘 해석하면 dp[n] = dp[n-1] + dp[n-2] + dp[n-3] 라는 점화식을 도출해 낼 수 있다.
2. 따라서 이를 이용해 문제를 풀면 된다.
3. 먼저 T를 입력받고, 문제에서 구하는 수가 11까지 이므로 해당 조합의 갯수들을 담을 벡터 dp를 12의 크기로 선언한다.
4. 인덱스는 0부터 시작되기 때문에 인덱스 11까지 사용하기 위해 편의상 크기를 12로 설정했다.
5. 결과들을 담을 output 벡터도 T의 크기로 선언해주고, 점화식 특성상 1,2,3은 값을 도출해낼 수 없기 때문에 기본값으로 구해서 세팅해준다.
6. 기본값 설정
6-1. 1 = 1 (1가지) => dp[1] = 1
6-2. 2 = 1+1, 2 (2가지) => dp[2] = 2
6-3. 3 = 1+1+1, 2+1, 1+2, 3 (3가지) => dp[3] = 4
7. 위와 같이 기본값을 설정한 뒤 4부터 11까지 반복하며 점화식 dp[n] = dp[n-1] + dp[n-2] + dp[n-3] 을 이용해 해당 값들을 구해준다.
8. T만큼 반복하며 n을 입력받고, output에 dp[n]을 저장해준다.
9. 모든 n에 대해 입력이 끝났다면 output의 원소를 하나씩 출력해준다.
<코멘트>
경우의 수를 나누어 조합을 이용해 겨우겨우 어렵게 풀었는데 다른 분의 답을 보니 허무했다ㅋㅋ
점화식만 알아내면 쉬운 문제였다!
dp 문제를 풀때는 점화식을 구하는 것을 먼저 생각해보자!
<제출결과>




